등굣길

등굣길

프로그래머스 42898 등굣길

  "등굣길" 이 맞다.

문제

계속되는 폭우로 일부 지역이 물에 잠겼습니다.
물에 잠기지 않은 지역을 통해 학교를 가려고 합니다.

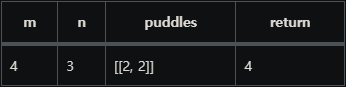
격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열
puddles이 매개변수로 주어집니다.
오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를
1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.

입출력 예시

접근

DP

어쩌다보니 문제가 DP라는 생각을 하지 못한 채 풀이를 시작하게 되어,
최단경로 라는 키워드로 BFS를 떠올렸다.

    Queue<int[]> queue = new LinkedList<>();
    queue.add(new int[]{0,0});
    int count = 0;

    int[][] directions = {{1, 0}, {0, 1}};

    while (!queue.isEmpty()) {
        int[][] pos = queue.poll();

        for (int[] direction : directions) {
            int nextX = pos.x + direction[0];
            int nextY = pos.y + direction[1];

            ...
        }
        if ( ) {
            count++;
        }
    }

그러다가 개수를 구하는 방법을 찾는 로직을 구현하기 어렵다고 느껴 접근 방식을 바꿔
DFS 라는 생각까지 미칠 찰나 문제의 카테고리를 확인하고 DP로 사고를 전환할 수 있었다.

이 전에 정수삼각형 을 풀면서 비슷한 방향의 풀이를 떠올려본적이 있었다.

결과적으로 DP와 1,000,000,007로 나눈 나머지 라는 키워드를 종합하여
DP와 모듈화 계산법을 적용해 처음부터 작성하기로 했다.

    public int solution(int m, int n, int[][] puddles) {
        long[][] map = new long[n + 1][m + 1];

        for (int[] puddle : puddles) {
            map[puddle[1]][puddle[0]] = -1;
        }
        map[1][1] = 1;

        ...

        return (int) (answer % 1000000007);
    }

향상된 for문을 이용하여 2차원 배열로 입력되는 puddles를 삼중 for문을 사용하지 않고도 map에 표시할 수 있었다.
또한 나머지 개수를 구할때 사용되는 모듈의 단위가 10억이었기에 int_MAX를 넘기지 않기 위해 Long으로 개수를 구한 뒤, return 직전에 캐스팅 해주었다.

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (map[i][j] == -1) { 
                continue;
            }
            if (i > 1 && map[i - 1][j] != -1) {
                map[i][j] += map[i - 1][j];
            }
            if (j > 1 && map[i][j - 1] != -1) { 
                map[i][j] += map[i][j - 1];
            }
        }
    }
    return (int) (map[n][m] % 1000000007);

집과 학교의 위치는 항상 동일하게 {1, 1}과 {m, n}이며 좌 상단에서 우 하단으로 이동하는 방식은 이중 for문을 이용한 2차원 배열의 완전 탐색과 일치한다.

효율성 테스트

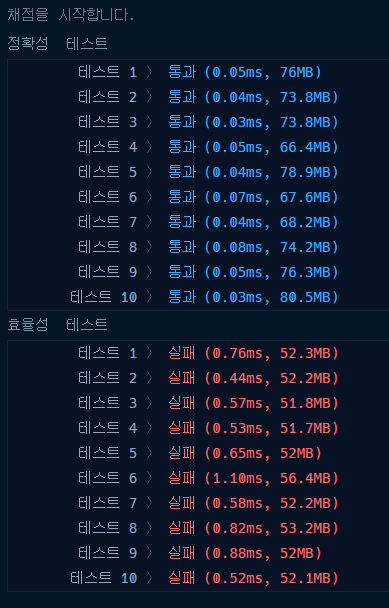
효율성 테스트에서 완전히 깨져버렸다.
모듈화 과정을 건너뛴다면 메모리를 조금 더 이용하더라도 처리 속도를 높일 수 있을 거란 기대에
int 대신 long을 이용해서 메모리부분에서 탈락인가 싶어 map의 자료형을 int[][]로 바꿨지만 오버플로우는 일어나지 않았다.

최대 경우의 수를 확인해보니 690,285,631 로, 애초에 오버플로우는 발생하지 않는 조건이었다.

결국return 직전에 캐스팅하려는 방법은 문제의 요구 사항과 다르다는것을 깨닫고 계산 과정에 %1000000007 을 넣어 모듈화 계산을 해주자 효율성 테스트를 통과할 수 있었다.

public class Solution {
    public int solution(int m, int n, int[][] puddles) {
        long[][] map = new long[n + 1][m + 1];

        for (int[] puddle : puddles) {
            map[puddle[1]][puddle[0]] = -1;
        }
        map[1][1] = 1;

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (map[i][j] == -1) { 
                    continue;
                }
                if (i > 1 && map[i - 1][j] != -1) {
                    map[i][j] += map[i - 1][j] % 1000000007;
                }
                if (j > 1 && map[i][j - 1] != -1) { 
                    map[i][j] += map[i][j - 1] % 1000000007;
                }
            }
        }
        return (int) (map[n][m] % 1000000007);
    }
}